Introduction
Fluid dynamics encompasses a wide range of phenomena, and while in our daily lives we often encounter continuous fluids, it is important to recognize that this is not universally true. Throughout the vast expanse of the universe, there exists a spectrum of states between continuous fluids and pure vacuum, necessitating the existence of transitional states. In different states, distinct sets of variables and equations should be employed to capture the system's behavior effectively. For example, the concept of temperature in fluid description loses its significance in the case of space containing only one atom. Presently, research in fluid dynamics primarily focuses on two distinct regimes, each posing unique challenges and opportunities for exploration. The first regime is continuous fluids, where fundamental variables such as density, velocity, and temperature can be employed to define the fluid's state. In this regime, the behavior of the fluid can be effectively described using classical fluid dynamics equations.The second regime is rarefied fluids, where the simple degrees of freedom provided by the fluid variables in the continuous regime are insufficient. In such cases, the Boltzmann equation acts as a powerful tool, capable of providing a more detailed description of the system.
Visualizing rarefied gases presents a challenge due to their inherently low density and microscopic nature. In contrast, the prominent field of nanoscience, visualization of atomic-scale structures is made possible through advanced tools like Scanning Electron Microscopes (SEMs).There are two primary reasons for the difficulty in visualizing rarefied gas samples on Earth. Firstly, generating such samples with extremely low densities poses a technical challenge in laboratory settings. Secondly, the development of devices capable of effectively visualizing and characterizing these gases is a complex task.Here is a figure to help develop a mental model and an overall picture of rarefied gases,
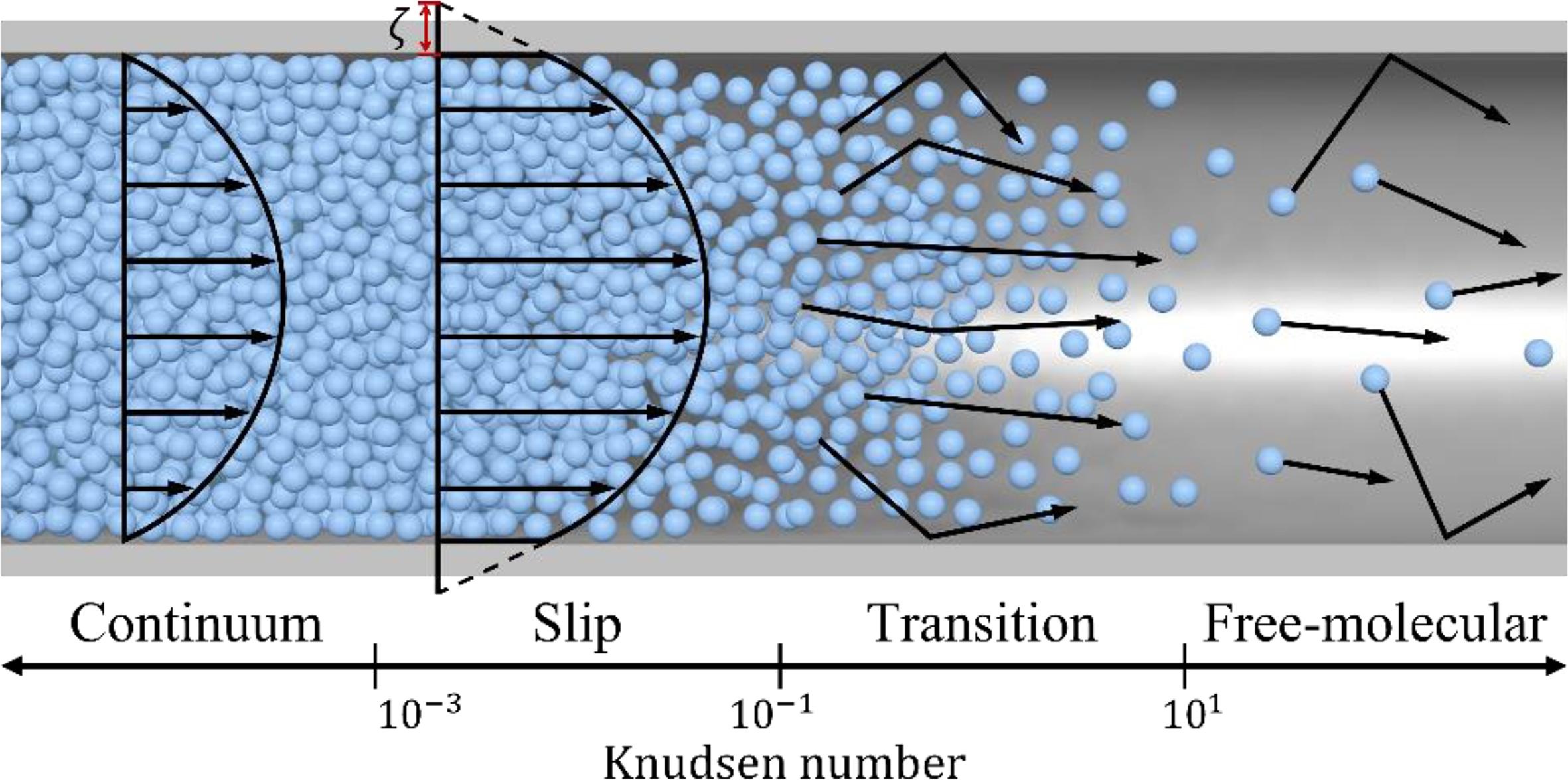
This is multiscale spectrum in nature. Another notable example of the multiscale phenomenon is the turbulence. It encompasses a wide range of scales, from the large-scale turbulence observed in flows to the smaller-scale eddies and vortices that form within them. This complex behavior is modeled by molecular dynamics, as depicted in the image below.

Multiscale phenomena in fluid mechanics indeed present significant challenges in modeling and numerical methods. In the continuum regime, fluid motion can be effectively described by the well-known Navier-Stokes equations, for which numerous numerical schemes have been developed. Among these schemes, the Riemann solver stands out as one of the most physically reliable methods.In the rarefied regime, where the fluid is sparse and the simple degrees of freedom provided by the continuum assumptions are no longer applicable, the Boltzmann equation becomes a crucial tool for describing nonequilibrium gas flow. To simulate such flows, there are primarily two types of numerical methods used.
The first type is the stochastic particle method, which employs discrete particles to capture statistical behavior of rarefied gas on a macroscopic level. This method relies on random sampling techniques and statistical analysis to approximate the solution of the Boltzmann equation. The direct simulation Monte Carlo (DSMC) method [4] is the most successful particle simulation method. The particle method requires low compuational memory and is highly efficient in rarefied flow computations since it can be regarded as the best adaptive strategy in phase space, especially for high-speed flows in multidimensional cases[3]. However, as a stochastic method, DSMC suffers statistical noise problem and may require additional computational resources to achieve accurate result by averaging. Besides, the DSMC method is limited by the mesh size, which is restricted by spatial scale of molecular mean free path. In the continuum regime where mean free path is extremely small, this constraint poses greate computational challenge. Significant efforts have been dedicated to mitigate statistical errors and address the stiffness problem encountered in the continuum regimes.The information preservation (IP) method, the low variance deviational simulation Monte Carlo(LVDSMC) method, and the momente guided Monte Carlo method have been developed to reduce the statistical error. The asymptotic preserving (AP) Monte Carlo methods have been developed so the the Ruler solution can be obtained in the hydrodynamic limit without the requirement on the time step and the mesh size as that in the traditional DSMC method [3].
The second type of numerical method for solving the Boltzmann equation is the deterministic method, which aims to discretize and directly solve the equation. Unlike the stochastic nature of the DSMC method, the deterministic method does not suffer from statistical noise. The deterministic method also demonstrates high computational efficiency, thanks to various acceleration techniques that can be employed. These techniques include implicit schemes, which allow for larger time steps and improved stability, and memory reduction methods, which optimize the memory usage during the simulation. Additionally, adaptive refinement methods can be implemented to dynamically adjust the mesh resolution based on the flow properties, enhancing both accuracy and efficiency.To overcome the stiffness problem associated with the collision term in the continuum regime, asymptotic preserving schemes have been developed. Most of them use implicit or semi-implicit method for the collision part. However, these fails to achieve second-order accuracy since they have the same numerical mechanism as the flux vector splitting (FVS) methods, where the intrinstic numerical dissipation is proportional to time step[5], which deteriorates the NS solution when a large time step is used. Xu et al[5] proposed the unified gas-kinetic scheme (UGKS) as AP scheme which couples the particles' free streaming and collision to remove the timestep restriction and achieve second-order accuracy. The multiscale transport modeling in UGKS has been applied in many transport problems later.
The particle method and the deterministic method have their own merits and disadvantages. If we can combine them together, it should be a great method. In the context of UGKS, such work has been implemented. The direct particle implementation of UGKS is the so-called unified gas-kinetic particle (UGKP) method[6]. The UGKP method mploys particles to represent the distribution function, as opposed to discrete distribution function bins used in the UGKS. It should be noted that, as a result of collisions, a portion of the particles will relax towards the local thermodynamic equilibrium state. In the context of the unified gas-kinetic wave-particle (UGKWP) method[7], this relaxation phenomenon is leveraged to calculate the numerical flux contributed by these equilibrium particles analytically. By doing so, the computational cost associated with particle sampling and advancement can be significantly reduced. The UGKWP method thus can adaptively become the particle simulation in collisionless regime and the hydrodynamic solver in the collisional regime, the same as the gas-kinetic scheme (GKS).
In this article, the construction of UGKWP method is introduced derived from UGKS and UGKP.
Reference
[1] Lee J, Kim J H. Statistical assessment of tangential momentum accommodation coefficient using internal flow rate model based on rarefied gas conditions[J]. Results in Physics, 2022, 43: 106130.
[2] https://www.reddit.com/r/CFD/comments/15kpzup/molecular_gas_dynamics_simulation_of_turbulence/
[3] Zhu Y, Liu C, Zhong C, et al. Unified gas-kinetic wave-particle methods. II. Multiscale simulation on unstructured mesh[J]. Physics of Fluids, 2019, 31(6).
[4] Bird G A. Molecular gas dynamics and the direct simulation of gas flows[M]. Oxford university press, 1994.
[5] Xu K, Huang J C. A unified gas-kinetic scheme for continuum and rarefied flows[J]. Journal of Computational Physics, 2010, 229(20): 7747-7764.
[6] Li W, Liu C, Zhu Y, et al. A unified gas-kinetic particle method for multiscale photon transport[J]. arXiv preprint arXiv:1810.05984, 2018.
[7] Liu C, Zhu Y, Xu K. Unified gas-kinetic wave-particle methods I: Continuum and rarefied gas flow[J]. Journal of Computational Physics, 2020, 401: 108977.

