Introduction
In physics, electromagnetic radiation (EMR) consists of waves of the electromagnetic (EM) field, which propagate through space and carry momentum and electromagnetic radiant energy (Because EM wave radiation can be conceptualized as a stream of photons, radiant energy can be viewed as photon energy). Types of EMR include radio waves, microwaves, infrared, visible light, ultroviolet, X-rays, and gamma rays, all of which are part of the electromagnetic spectrum. Electromagnetic waves of different frequency are called by different names since they have different sources and effects on matter.
Electromagnetic waves are emitted by electically charged particles undergoing acceleration. One of such case is oscillating electrical dipole. From Maxwell equation we know, time-varying electric field can produnce magnetic field and vice versa. Therefore, as long as we have such electric field, we can radiate EM wave and propagate out. A basic EM radiation model is oscillating electric dipole model where \(\boldsymbol{p}=\boldsymbol{p}_0 cos(\omega t)\). EMR is associated with these radiated EM waves that are free to propagate themselves ("radiate") without the continuing influence of the moving charges that produced them, because they have achieved sufficient distance from those charges. Thus EMR is sometimes referred to as the far field. In this language, the near field refers to EM fields near the charges and current that directly produced them, specifically electromagnetic induction and electrostatic induction phenomena.
In quantum mechanics, an alternate way of viewing EMR is that it consists of photons, uncharged elementary particles particles with zero rest mass which are the quanta of the electromagnetic field, responsible for all electromagnetic interactions.
Derivation of photons
The research leading to an understanding of the nature of light and the emission and absorption processes has been of paramount importance. It led from a beginning in 1900 to the development of quantum physics, reaching a high peak in the 1920s and a fruition towards the mid-century years with the completion of the very successful Quantum Electrodynamic(QED) theory.
The wave-particle duality
A particle on the classical view is a concentration of energy and other properties in space and time,whereas a wave is spread out over a larger region of space and time. The question whether light are streams of particles (corpuscles) or waves is a very old one. This “either – or” formulation was classically natural and alien to the advanced “both – and” even the “neither – nor” solution of today. Early in the nineteenth century experiments were suggested and made to show that light is a wave motion. A key figure in this endeavour was Thomas Young, one of the most intelligent and clever scientists ever to live, who studied diffraction and interference of light already in 1803 with results that gave strong support to the wave theory of Christian Huygens as opposed to the particle or corpuscular theory of Isaac Newton.Further contributions were made by many other researchers, among them Augustin Jean Fresnel, who showed that light is a transverse wave.
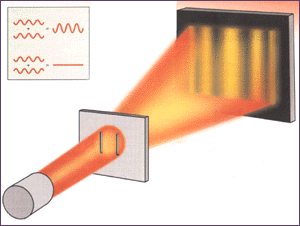
Newton’s theory of light had seemed suitable to explain the straight-line casting of sharp shadows of objects placed in a light beam. But wave theory was needed to explain interference where the light intensity can be enhanced in some places and diminished in other places behind a screen with a slit or several slits. The wave theory is also able to account for the fact that the edges of a shadow are not quite sharp.
The mathematical theory of electromagnetism by James Clerk Maxwell, set up in 1864, led to the view that light is of electromagnetic nature, propagating as a wave from the source to the receiver. Heinrich Hertz discovered experimentally the existence of electromagnetic waves at radio-frequencies in the 1880s. Maxwell died in 1879 and Hertz died only 37 years old in 1894, two years before Alfred Nobel’s death.
At the end of the 19th century, which also is the time when the Nobel Prizes were instituted, the wave nature of light seemed definitely established. Thus the decisive research into the wave nature of light came too early to be considered for Nobel Prizes. However, there is one exception – the case of X-rays.
Discoveries relating to the particle nature of light belong to our century and thus one might expect Nobel Prizes be awarded for such achievements. This is almost true – but the Nobel archive tells a more complicated story as will be uncovered below.
The Nobel Prizes for X-rays
The discovery of X-rays by Wilhelm Conrad Röntgen in 1895 was honoured by the first Nobel Prize in Physics in 1901. Röntgen had shown among many other things that X-rays like light, were propagating in straight lines but in contrast to light very penetrating through matter. Röntgen foresaw the importance to medical science of his discovery.
This discovery had so many important consequences that it well fulfills the stipulation in Alfred Nobel’s will of having “conferred the greatest benefit on mankind”. After 1912 when Max von Laue, who was awarded the 1914 Nobel Prize in Physics, had suggested and observed refraction of X-rays did the wave picture obtain general acceptance.
The interatomic distances in a crystal match quite well the wavelengths of X-rays. von Laue worked out the theory for diffraction in a 3-dimensional grating and made predictions, which were verified by the experiments of W. Friedrich and P. Knipping.
The nature of the new radiation, discovered by Röntgen in 1895, was by no means clear in 1901 when he was awarded the Nobel Prize. In the beginning the only property which was found in common with light was that of propagation in straight lines. As late as 1910 a heated debate occurred between Barkla and Bragg; one defending the idea that X-rays are waves like light, the other that they consist of streams of little bullets.
The Nobel Lecture by Arthur H. Compton in 1927 was entitled “X-rays as a Branch of Optics”. It begins, “One of the most fascinating aspects of recent physics research has been the gradual extension of familiar laws of optics to the very high frequencies of X-rays, until at the present there is hardly a phenomenon in the realm of light whose parallel is not found in the realm of X-rays. Reflection, refraction, diffuse scattering, polarization, diffraction, emission and absorption spectra, photoelectric effect, all of the essential characteristics of light have been found also to be characteristic of X-rays. At the same time it has been found that some of these phenomena undergo a gradual change as we proceed to the extreme frequencies of X-rays, and as a result of these changes in the laws of optics we have gained new information regarding the nature of light.
Evidence for the particle nature of light
In physics textbooks two phenomena are usually quoted demonstrating the particle nature of light: 1) the photoelectric effect and 2) the Compton scattering of X-rays.
In some not so critical texts a third circumstance is erronously quoted, namely Planck‘s discovery of energy quanta, which he did in his analysis of heat radiation. The Nobel Committee honoured this monumental discovery by the Physics Prize in 1918, but did not make the mistake to give Planck credit for having discovered the particle nature of light.
The Nobel Prize for Physics to Max Planck
Planck’s discovery of what is called Planck’s constant \(h\), was emphasized as motivation for his prize in 1918. This new constant of nature (with the dimension of energy multiplied by time) connects the quantum of energy with the frequency of light,\(\nu\), through the formula \(E = h \nu\).In the presentation at the Nobel Prize ceremony in 1918 it was said , “The product \(h\nu\) is actually the smallest amount of heat which can be radiated at the vibration frequency \(\nu\).” Planck himself resisted the idea that light in vacuum propagates as particles, later on called photons.
As will be clear from the following, the Nobel Committee for Physics did not recognise the particle nature of light neither when awarding the 1921 Prize (awarded in 1922) to Albert Einstein “for his discovery of the law of the photoelectric effect,” nor when in 1927 awarding Arthur Holly Compton the Physics Prize “for his discovery of the effect named after him.”
The 1921 Nobel Prize to Albert Einstein (awarded in 1922)
Albert Einstein in 1905 drew the conclusion that light sometimes behaves as particles through an ingenious statistical analysis of Wien‘s formula for the wave length distribution of heat radiation.
Einstein saw that his new idea would provide a natural explanation of the photoelectric effect, i.e. the emission of electrons from metal surfaces illuminated by light. The wave theory of light was quite unable to do so. The motivation for the Nobel Prize to Einstein in 1922 was based on his discovery of the law of the photoelectric effect.
Einstein repeated the statistical calculation with Planck’s formula as the basis, which is more general than Wien’s, and drew the conclusion that both the concept of waves and the concept of particles in the light heat bath in a cavity are called for. During a seminar discussion at the Prussian Academy in Berlin in 1909 Einstein used this new calculation in order to try to convince Planck and others present of the necessity to consider light also as consisting of a number of independent particles.
As is well known Einstein did not get the Nobel Prize for his relativity theories due to strong disbeliefs in those theories among some influential members of the Royal Swedish Academy of Sciences. The 1911 Nobel Laureate in Physiology or Medicine Allvar Gullstrand was of the opinion that the correctness of Einstein’s special relativity theory rested on belief – not proven facts, and the general relativity theory could in his opinion not stand a critical analysis.
Now, does not the prize to Einstein imply that the Academy recognised the particle nature of light? The Nobel Committee says that Einstein had found that the energy exchange between matter and ether occurs by atoms emitting or absorbing a quantum of energy, \(h\nu\).
As a consequence of the new concept of light quanta (in modern terminology photons) Einstein proposed the law that an electron emitted from a substance by monochromatic light with the frequency \(\nu\) has to have a maximum energy of \(E = h\nu-P\), where \(P\) is the energy needed to remove the electron from the substance.
Robert Andrews Millikan carried out a series of measurements over a period of 10 years, finally confirming the validity of this law in 1916 with great accuracy. Millikan had, however, found the idea of light quanta to be unfamiliar and strange.
The Nobel Committee avoids committing itself to the particle concept. Light-quanta or with modern terminology, photons, were explicitly mentioned in the reports on which the prize decision rested only in connection with emission and absorption processes. The Committee says that the most important application of Einstein’s photoelectric law and also its most convincing confirmation has come from the use Bohr made of it in his theory of atoms, which explains a vast amount of spectroscopic data.
In his theory of the atoms Bohr used the law of Einstein as the basic condition for the frequency of light emitted or absorbed, when an atom makes a transition between two quantized energy levels \(E_1\) and \(E_2\) , in the form \(\nu = (E_1 - E_2)/h\) , which in modern texts is nothing but basic energy conservation with a photon emitted or absorbed as the case may be. Bohr, however, resisted the concept of photons for many years, until about 1925. In his 1922 Nobel lecture Bohr expressed his opposition in the following words:“In spite of its heuristic value the hypothesis of light quanta, which is quite irreconcilable with the so-called interference phenomena, is not able to throw light on the nature of radiation.” Einstein was invited to receive his prize at the same event, but could not come, because of his journey to Japan. Thus the world missed the opportunity to witness an early discussion between these two giants of physics about the nature of light.
The connection between Einstein and Bohr, which the Nobel Committee for physics saw, was made manifest by the two Nobel Prizes decided in 1922: the reserved one from the earlier year to Einstein and the current one to Bohr.
附:光电效应理论概述
光束里的光子所拥有的能量与光的频率成正比。假若金属里的电子吸收了一个光子的能量,而这能量大于或等于某个与金属相关的能量阈值(称为这种金属的逸出功),则此电子因为拥有了足够的能量,会从金属中逃逸出来,成为光电子;若能量不足,则电子会释出能量,能量重新成为光子离开,电子能量恢复到吸收之前,无法逃逸离开金属。增加光束的辐照度(光束的强度)会增加光束里光子的密度,在同一段时间内激发更多的电子,但不会使得每一个受激发的电子因吸收更多的光子而获得更多的能量。换言之,光电子的能量与辐照度无关,只与光子的能量、频率有关。
被光束照射到的电子会吸收光子的能量,但是其中机制遵照的是一种非全有即全无的准则,光子所有能量都必须被吸收,用来克服逸出功,否则这能量会被释出。假若电子所吸收的能量能够克服逸出功,并且还有剩馀能量,则这剩馀能量会成为电子在被发射后的动能。
逸出功 \(W_0\) 是从金属表面发射出一个光电子所需要的最小能量。如果转换到频率的角度来看,光子的频率必须大于金属特征的极限频率,才能给予电子足够的能量克服逸出功。逸出功与极限频率 \(\nu_0\) 之间的关系为 \(W_{0}=h\nu _{0}\) 其中, \(h\) 是普朗克常数, \(h\nu_0\) 是光频率为 \(\nu_0\) 的光子的能量。
克服逸出功之后,光电子的最大动能 \(E_{\mathrm {max} }\) 为 \(E_{\mathrm {max} }=h\nu -W_{0}=h(\nu -\nu _{0})\) 其中, \(h\nu\) 是光频率为 \(\nu\) 的光子所带有并且被电子吸收的能量。 实际物理要求动能必须是正值,因此,光频率必须大于或等于极限频率,光电效应才能发生。
The Nobel Prize to Arthur Holly Compton (1927)
Early in 1923 Arnold Sommerfeld visited the USA and wrote to Bohr: “The most interesting thing ..is the work of Compton in St Louis…. After it the wave theory of X-rays will become invalid.”
Compton had followed up an observation that some parts of X-rays were scattered away from the beam direction with a longer wave length than the incoming radiation.He measured the shift in wave-length very accurately. The shift is impossible to understand on classical wave theory. Compton’s own explanation for the scattering process was as in terms of a collision between two particles – one being a free electron, the other a photon.
Based on quantum theory and relativistic kinematics Compton calculated what shift of wave length to expect on this theory using the laws of energy and momentum conservation. His measurements agreed perfectly with the predictions.Compton used an X-ray spectrometer for accurate measurements of the wave-length of the scattered radiation, which consists of two components – one shifted and one with no shift. The shifted component is due to scattering against free or almost free electrons, so that they may recoil, thereby taking up momentum and a sizeable amount of energy, whereas the unshifted component is due to scattering against bound electrons, in which case the whole atom or even crystal takes up momentum but only a negligible amount of energy.
The understanding of how such a spectrometer as used by Compton functions is based on the wave theory of X-rays. By this he found that X-rays scatter as particles. This fact illustrates clearly the dual nature of light.
Compton was awarded the Nobel Prize for Physics in 1927, sharing it with C.T.R.Wilson for his cloud chamber, with which Wilson had observed the recoil electrons from the X-ray beam, thus giving strong support for the validity of the Compton process.
Did the Academy now finally award the prize for the discovery of the particle nature of light? The answer is no.
In the evaluation report one finds a sentence saying that Compton’s theory must now be considered obsolete in view of the latest theories. Thus the particle picture is not accepted.
The position taken by the Nobel Committee is understandable, since at the time of Compton’s Nobel Prize there was no good theory for the differential cross section based on the photon concept. Such theories were still in the future. But there were theories based on the wave picture, treating both the electrons and the X-radiation as waves, also giving the correct wave length shift.
附: 康普顿效应简介 康普顿效应首先在1923年由美国物理学家阿瑟·康普顿观察到,并在随后的几年间由他的研究生吴有训证实了其普遍性。康普顿因发现此效应而获得1927年的诺贝尔物理学奖。
这个效应反映出光不仅仅具有波动性。此前汤姆孙散射的经典波动理论并不能解释此处波长偏移的成因,必须引入光的粒子性。这一实验说服了当时很多物理学家相信,光在某种情况下表现出粒子性,光束类似一串粒子流,而该粒子流的能量与光频率成正比。
在引入光子概念之后,康普顿散射可以得到如下解释:电子与光子发生弹性碰撞(弹性碰撞产生的非弹性散射),电子获得光子的一部分能量而反弹,失去部分能量的光子则从另一方向飞出,整个过程中总动量守恒,如果光子的剩余能量足够多的话,还会发生第二次甚至第三次弹性碰撞。
康普顿散射可以在任何物质中发生。当光子从光子源发出,射入散射物质(一般指金属)时,主要是与电子发生作用。如果光子的能量相当低(与电子束缚能同数量级),则主要产生光电效应,原子吸收光子而产生电离。如果光子的能量相当大(远超过电子的束缚能)时,则我们可以认为光子对自由电子发生散射,而产生康普顿效应。如果光子能量极其大(>1.022百万电子伏特)则足以轰击原子核而生成一对粒子:电子和正电子,这个现象被称为成对产生。
由于光子具有波粒二象性,因此,应该可以用波动理论诠释这效应。埃尔温·薛定谔于1927年给出半经典理论。这理论是用古典电动力学来描述光子,用量子力学来描述电子。
Prizes for the discoveries of the dual nature of matter
The dual nature of light has been extended to a similar duality in matter as well. Electrons and atoms were originally considered as corpuscles. In 1929 Prince Louis-Victor de Broglie was awarded the Nobel Prize for Physics for “his discovery of the wave nature of electrons”.Experimental proofs were given by Clinton Joseph Davisson, New York, and Sir George Paget Thomson from London. They were jointly awarded the Nobel Physics Prize in 1937. Ever since Erwin Schrödinger in 1925 discovered the nonrelativistic wave equation for the electron wave mechanics has been a valuable tool for the natural sciences. Schrödinger was awarded the Nobel Prize in Physics in 1933.
The Nobel Committee had earlier carefully avoided being explicit about the particle nature of light, but did not hesitate to be explicit about matter sometimes behaving as waves. Bohr’s idea about complementarity had been presented two years earlier, so in the presentation speech at the Nobel award ceremony in 1929 one finds a reflection of that in the following sentences: “It thus seems that light is at once a wave motion and a stream of corpuscles. Some of its properties are explained by the former supposition, others by the second. Both must be true.”
Nobel Prize for theories solving the duality problem of light
With the advent of quantum mechanics in 1925-1926 the possibility opened for a solution to the duality problem.
Paul Dirac published in 1927 a mathematical theory for the interaction between electromagnetic fields, such as light or X-rays, and charged particles with both aspects of light inbedded – it was a theory of quantised fields. Further contributions were given by several physicists and was generalized also to matter fields and is today an indispensable tool for treating fundamental interactions of any kind (strong, weak or electromagnetic). Three of the pioneers, Dirac, Werner Heisenberg and Wolfgang Pauli, were awarded Nobel Prizes for Physics but for other achievements.
The initial version of the Dirac theory combining wave and particle aspects of light, is useful only to a first approximation.Calculations give reasonable agreements with experiments;one such is the differential cross section for Compton scattering. However, when attempting more accurate calculations, which are needed in specific cases, the results become crazy and in fact infinite. The situation was remedied in the 1940s by works of Sin-Itiro Tomonaga, Julian Schwinger and Richard Feynman,who were jointly awarded the Nobel Prize for Physics in 1965.Thanks to their work one now has one of the most beautiful and accurate theories mankind has achieved in this area, the QED or Quantum Electro-Dynamics.It is expressed in mathematical language, perfect for this kind of enterprise, going beyond the everyday dialectic of wave and particle duality to the synthesis of a quantum field.
Richard Feynman based his version of quantum mechanics on the concept of “path integral”. He proposed that the transition probability amplitude be calculated by summing contributions from each alternative space-time trajectory of the particles with specific phase factors.From this approach Feynman derived a graphical representation of the amplitudes of the QED, which made the theory much easier to handle. In Feynman graphs photons and electrons are pictorially given as lines in a space-time diagram.Interactions with exchange of energy-momentum and other properties occur in such space-time points, where particle lines meet. Feynman graphs are nowadays the standard method used to calculate theoretical predictions.
The QED theory is, however, too advanced for many practical applications and usually given only as advanced graduate courses. Every new physics student therefore has to struggle with the duality problem, allowing the simultaneous existence of both particle and wave concepts and holding that the two are mutually exclusive (as Niels Bohr formulated in his Complementarity Principle of 1927).
A small, elementary book based on popular lectures by Feynman, can be recommended: “QED. The Strange Theory of Light and Matter” by Richard Feynman (Princeton University Press, 1985), in which Feynman gives the essence of his version of QED in simple language and elegant manner, even describing how the laws of geometrical optics can be derived from the QED theory.
The wave-particle duality in one and the same experiment
Experiments with beams of light or of electrons have been made such that both aspects – waves and particles – are observed.For interference to occur it is among other things also necessary for the beam to have available more than one path from source to detector (e.g. a screen). Interference is explained by the wave picture. When the beam intensity is sufficiently low and the detector suitable the impact of particles one by one can be observed. The energy quanta are then localised as if particles in space and time.
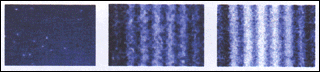
Detector output is displayed on a TV-monitor shown here in a set of frames; the first frame is early on; the last after a long time of impact collection. The interference pattern is slowly built up by impacts of individual particles.
Modern high technology makes possible quite intricate experiments with light or with electrons or atoms, which can appear mind-boggling when described by either the wave picture or the particle picture.
Postscript
The photon is the field quantum (particle) acting as the communicator of force between charged particles. It has successfully been imbedded in a larger context together with the three communicators of the weak force – (W+, W– Z0). The latter three are very heavy particles, whereas the photon is massless. Together they are the communicators of the forces of the unified electroweak interaction.
Nobel Prizes were awarded in 1979 to the three theoretical physicists Sheldon Glashow, Abdus Salam, and Steven Weinberg “for their contributions to the theory of the unified weak and electromagnetic interactions between elementary particles, including, inter alia, the prediction of the weak neutral current” and in 1984 to Carlo Rubbia and Simon van der Meer “for their decisive contributions to the large project, which led to the discovery of the field particles W and Z, communicators of weak interaction”.
Electromagnetic radiation in thermal equilibrium inside an enclosure
Let us consider the electromagnetic radiation (or in quantum-mechanical language, the assembly of photons) which exists in thermal equilibrium inside an enclosure of volume \(V\) whose walls are maintained at the absolute temperature \(T\). In this situation photons are continously absorbed and reemitted by the walls; it is, of course, by virtue of these mechanisms that the radiation inside the container depends on the temperature of the walls.
